深入了解Mysql【九】B+树

B+树由B树和索引顺序访问方法（ISAM,MyISAM引擎的最初参考数据结构）演化而来。

1、定义

• B+树是为磁盘或者其他直接存储辅助设备设计的一种平衡查找树。
• 所有的记录都按照键值的大小顺序存放在同一层的叶子节点上，由各叶子节点指针连接。
• m阶B+树表示了内部结点最多有m-1个关键字（或者说内部结点最多有m个子树），阶数m同时限制了叶子结点最多存储m-1个记录。

2、优势

• 非节点存储更多的key，使得查询的IO次数更少。
• 数据都存储在叶子节点，查询性能稳定。
• 所有叶子节点是有序链表，便于范围查询。

3、插入

分为三种情况：

• 叶子节点Page未满，索引Page未满。
  直接将数据插入到叶子节点Page。
• 叶子节点Page满，索引Page未满。
  拆分叶子节点Page,将中间的数据的键值进位到索引Page。
• 叶子节点Page满，索引Page满。
  拆分叶子节点Page,将中间的数据的键值进位到索引Page;
  拆分满了的索引Page，将中间数据进位到新的索引Page。

例子：参考于B树和B+树的插入、删除图文详解。
主要是不想画图了。
一颗5阶B+树的插入：
（5阶B+树的节点，最少2个key,最多4个key）

1. 空树中插入5
   

2. 依次插入8，10，15
   

3. 插入16
   
   插入16之后，叶子节点Page满了，需要将中间的数据key:10进位到新的索引Page：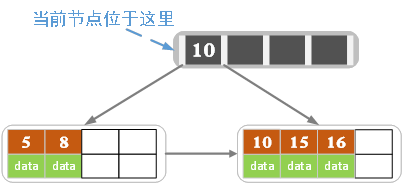
   

4. 插入17
   

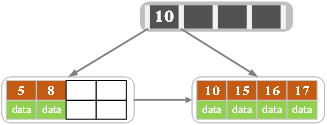
5. 插入18
   
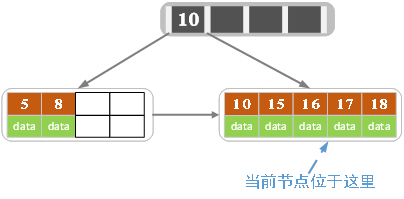
   插入18之后，当前叶子节点Page满，索引key:16向上进位。当前节点Page分裂为两块：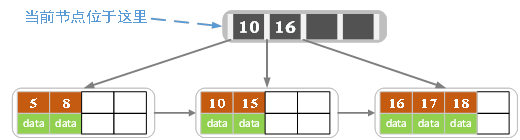
   

6. 插入若干数据后
   

7. 插入7
   
   当前叶子节点需要分裂，索引key:7需要进位。
   

碰巧索引Page也满了，需要分裂成两块，索引key:16进位：

插入结束。

4、删除

B+树使用填充因子来控制树的删除变化，填充因子的最小值为50%。
B+树删除的三种情况：

• 叶子节点 不小于 填充因子，索引节点 不小于 填充因子。
  直接将记录从叶子节点删除，如果该节点还是索引页的节点，则用该节点的右节点代替。
• 叶子节点 小于 填充因子，索引节点 不小于 填充因子。
  合并叶子节点与他的兄弟节点，同时更新索引页。
• 叶子节点 小于 填充因子，索引节点 小于 填充因子。
  合并叶子节点和他的兄弟节点，更新索引页，合并索引页与他的兄弟节点。

例子依然参考大神的：B树和B+树的插入、删除图文详解。

1. 初始状态
   

2. 删除22,删除后结果如下图
   
   删除后，叶子节点与索引节点无变化，属于上面第一种情况。

3. 删除15，删除后的结果如下图所示
   
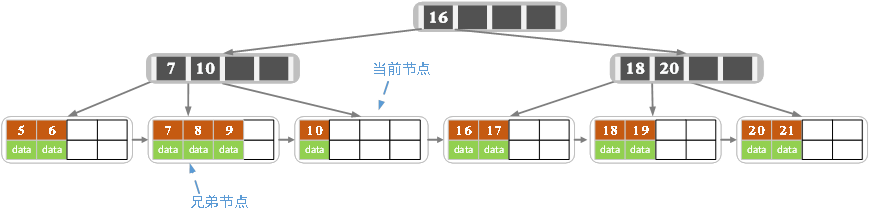
   删除后，叶子节点小于填充因子，从兄弟节点借过来一个9，更新索引页。
   

4. 删除7
   
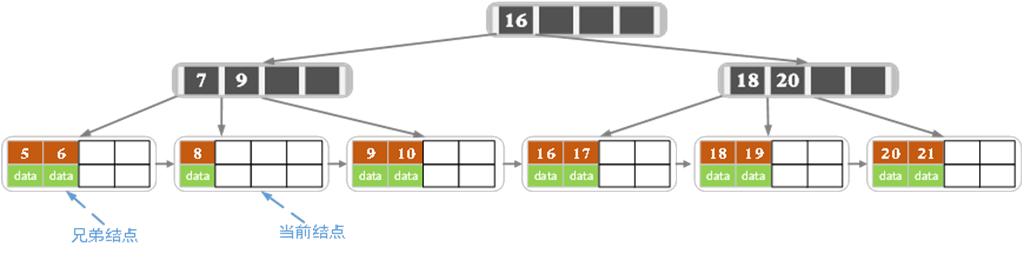
   删除后，当前节点小于填充因子，兄弟节点也没有余粮，所以合并兄弟节点，并更新索引页，这时候是这样：
   
   发现索引页中的节点也小于填充因子，兄弟节点也没有富余，所以兄弟节点合并，更新更上一层索引页：
   
   删除结束。

参考

B树和B+树的插入、删除图文详解
b+树图文详解
《MySQL技术内幕：InnoDB存储引擎 第二版》