本篇文章全部摘抄翻译于:javatpoint
学习的进程终于到了Mysql的索引部分，在这部分的开始，必须要简单的看一下数据结构和算法相关的知识点。
下面依次简单的看一下Tree、Binary Tree、Binary Search Tree、AVL Tree、B Tree、B+ Tree。

1、Tree

  • 树是一种数据结构，包含一个或者多个数据节点的集合，其中一个节点被指定为树的根，其余节点被称为根节点的子节点。
  • 除根节点以外的其他节点均被划分为多个非空集，其中每个空集都称为子树。
  • 树的节点之间的关系为父子关系或者姐妹关系。
  • 在一般树中，一个节点可以有任意数量的子节点，但只能有一个父节点。

下图显示了一棵树，其中节点A是树的根节点，而其他节点可以视为A的字节。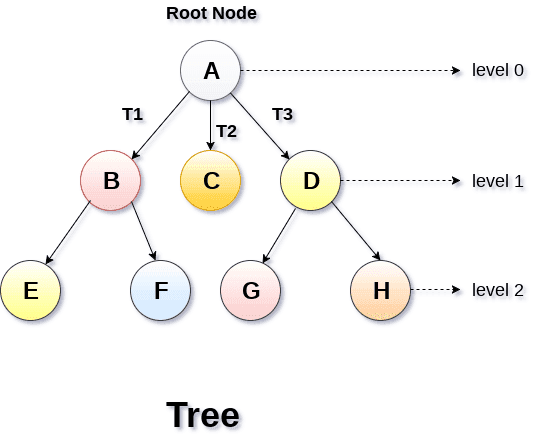
tree.png

基本术语

  • 根节点
    根节点是树层次结构中的最高的节点，根节点没有任何父节点。
  • 子树
    如果根节点不为空，则树T1\T2\T3被称为根节点的子树。
  • 叶子节点
    没有任何字节点的树的节点称为叶子节点。
  • 路径
    连续边的顺序成为路径，如上图中，到节点E的路径为A->B->E。
  • Degree
    节点拥有的子节点的个数，如B节点的度为2，叶子节点的度为0。
  • Level Number
    根节点的级别为0，子节点比父节点高一个等级。

2、Binary Tree

2.1、定义

二叉树是一种特殊类型的通用树，其中每个节点最多可以有两个子节点。
有三个组成部分：

  • 节点的根
  • 左子树，也是二叉树
  • 右子树，也是二叉树

下图显示了一个二叉树：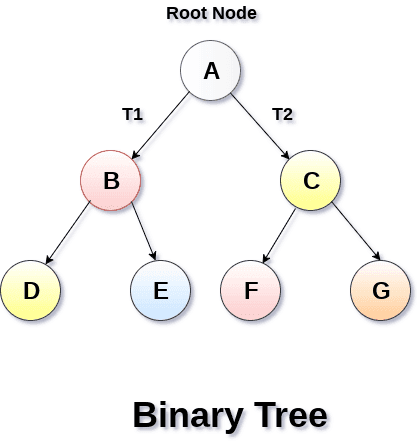
binary-tree.png

2.2、类型

2.2.1、严格的二叉树

每个非叶子节点都包含非空的左右子树。每个非叶子节点的度始终为2，
具有n个叶子节点的严格二叉树将有（2n-1）个节点。
如图：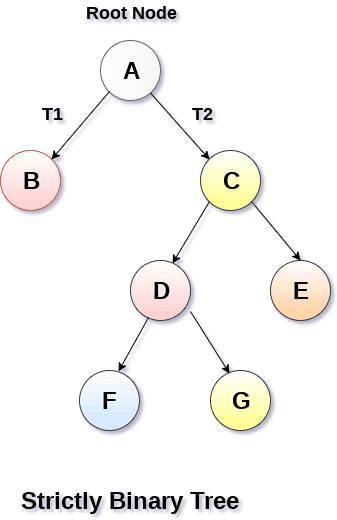
strictly-binary-tree.png

2.2.2、完整的二叉树

所有的叶子节点都处于同一级别。
如图：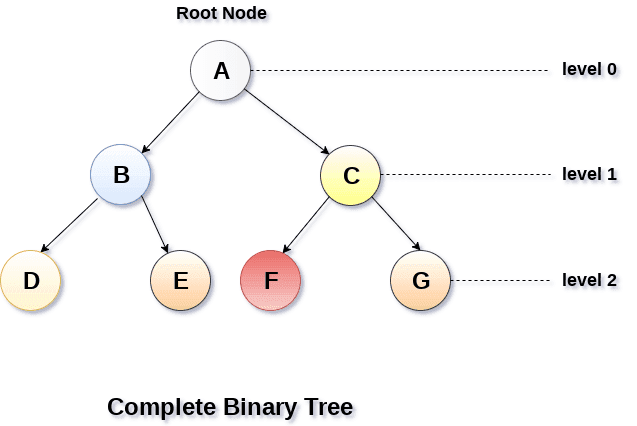
complete-binary-tree.png

其实还有完美二叉树、完全二叉树、完满二叉树的区别，
上面这个图写的是完全二叉树，其实应该写Full/Strictly Binary Tree。

2.3、遍历

  • 前序遍历
    先遍历根节点，然后分别遍历左子树和右子树。
  • 中序遍历
    先遍历左子树，然后遍历根节点，在遍历右子树。
  • 后序遍历
    先遍历左子树，然后遍历右子树，最后遍历根节点。

也就是遍历方式是根据根节点来确认的，根节点第一个遍历，就是前序遍历。
根节点中间遍历，就是中序遍历，根节点最后，就是后序遍历。

3、Binary Search Tree

3.1、定义

  • 二叉查找树为有序二叉树。
  • 左子树的所有节点的值，小于根节点的值。
  • 右子树的所有节点的值，大于根节点的值。

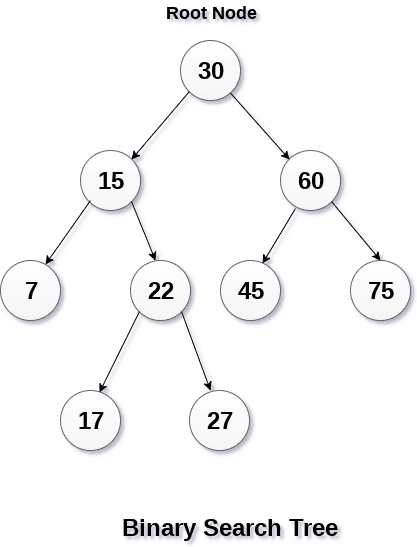
binary-search-tree.png

3.2、优点

  • 查找、插入、删除操作不错。
  • 充分利用了二分查找算法。

3.3、例子

问题：使用以下数据元素创建二叉查找树。
43、10、79、90、12、54、11、9、50

  • 将43插入到树中作为树的根。
  • 读取下一个元素（如果小于根节点元素），则将其插入到左子树的根。
  • 否则，将其插入为右侧子树右侧的根。

下图显示了使用给定元素创建BST的过程。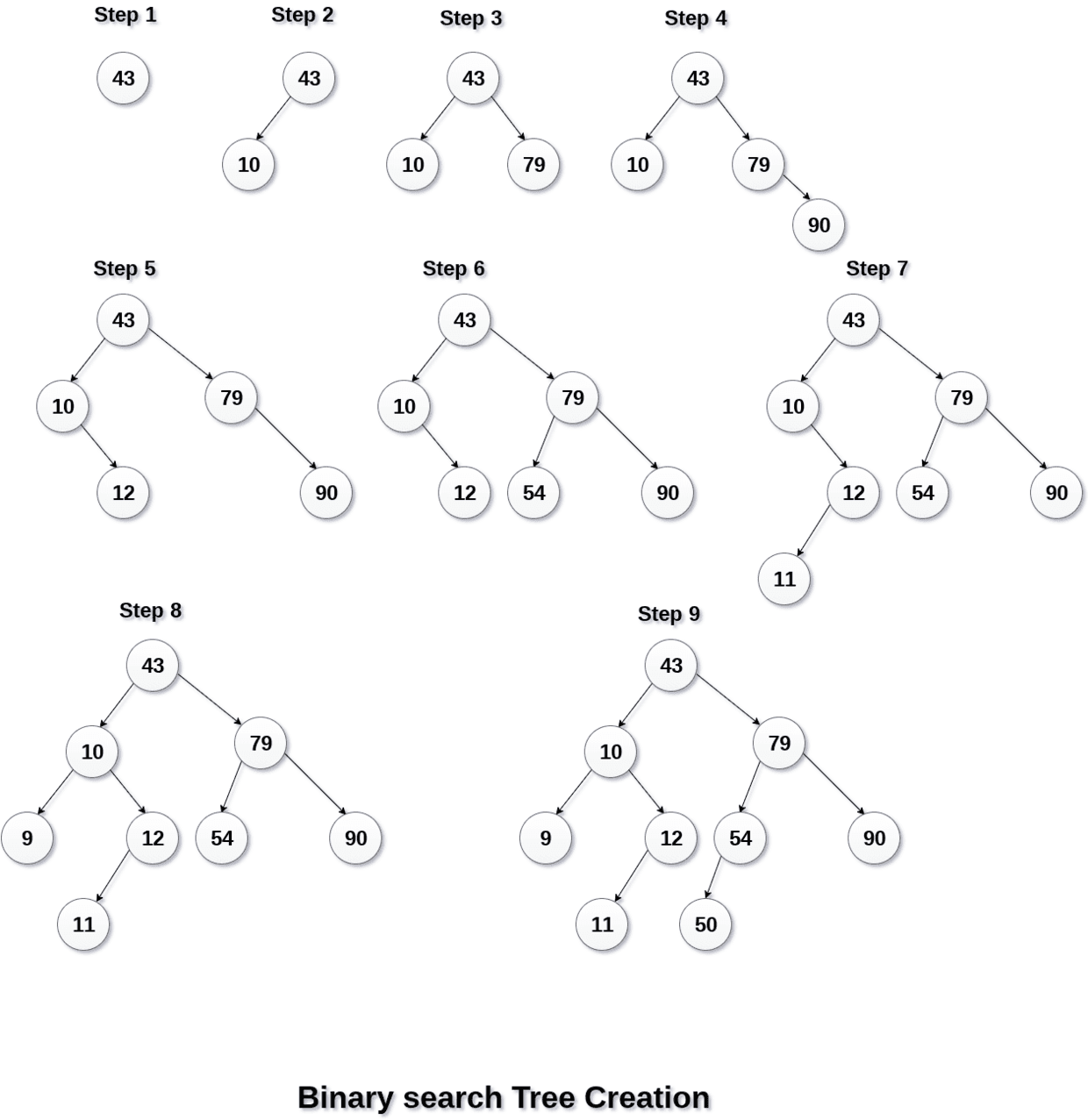
binary-search-tree-creation.png

4、AVL Tree

AVL树是由GM Adelson-Velsky和EM Landis于1962年发明的。为了纪念其发明者，该树被命名为AVL。
AVL树是高度平衡的二叉查找树。
平衡系数（k）=高度（left（k））-高度（right（k））
如图：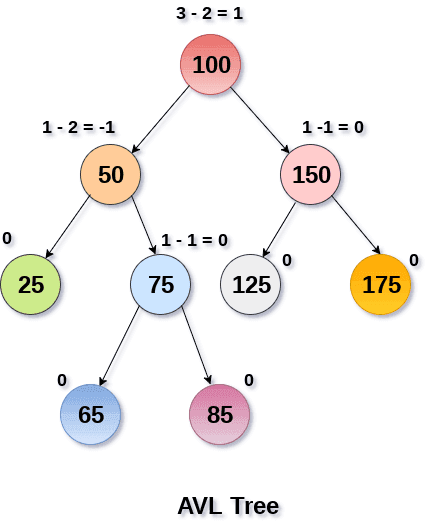
avl-tree.png

5、B Tree

一棵m阶的B树的特点：
阶数表示了一个结点最多有多少个孩子结点，也就是Degree的意思。

  • 树中的每个结点最多含有m个孩子；
  • 除了根结点和叶子结点，其他结点至少有[ceil(m / 2)（代表是取上限的函数）]个孩子；
  • 若根结点不是叶子结点时，则至少有两个孩子（除了没有孩子的根结点）
  • 所有的叶子结点都出现在同一层中，叶子结点不包含任何关键字信息；

下图展示了4阶B树：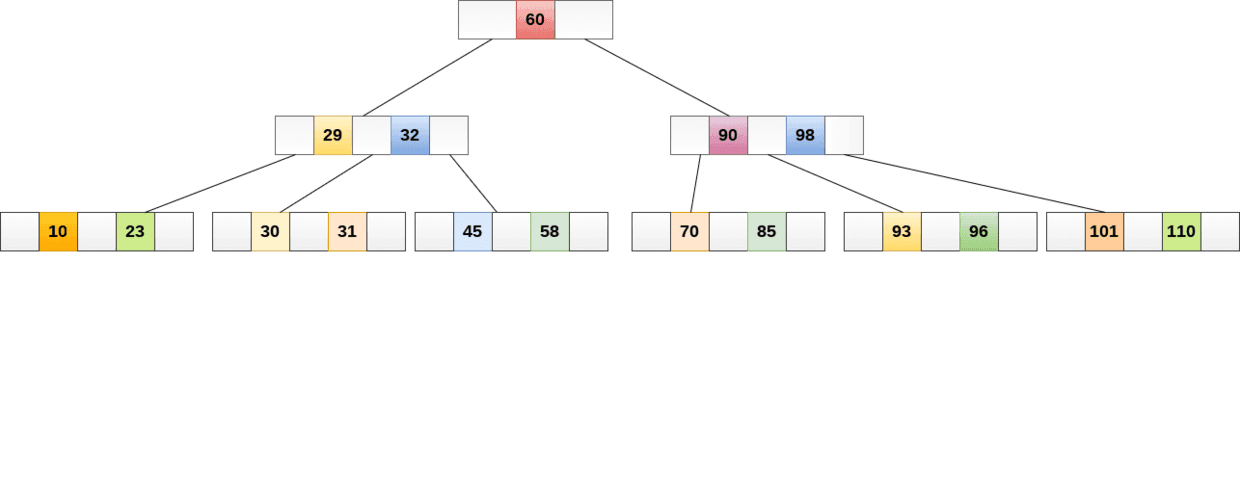
b-tree.png

6、B+ Tree

6.1、定义与特点

  • B+树是B树的扩展，插入，删除与搜索性能都很不错。
  • 在B数中，键和记录都可以存储在内部节点月叶子节点中，而B+树中，记录只能存储在叶子节点，内部节点只能存储键。
  • B+树的叶子节点以单链表的形式连接在一起，以使得搜索查询更高效。
  • B+树用于存储无法存储在内存中的大量数据，B+树的内部节点存储在主存中，叶子节点存储在辅助存储器中。
  • B+树的内部节点成为索引节点。

下图显示了3级B+树：
b-plus-tree.png

6.2、优势

  1. 可以在相同数量的磁盘访问中提取记录。
  2. 与B树相比，树的高度保持平衡并且较小。
  3. 我们可以依次或直接访问B +树中存储的数据。
  4. 键用于索引。
  5. 由于数据仅存储在叶节点上，因此搜索查询速度更快。

6.3、B树与B+树的对比

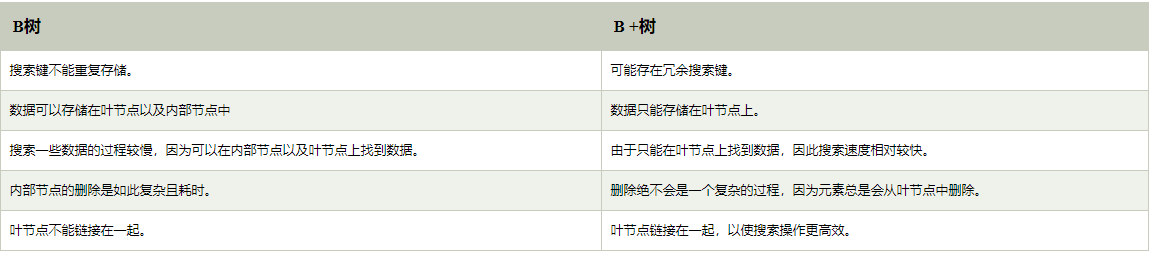
B树与B+树.png

6.4、插入

步骤1：将新节点插入为叶节点
步骤2：如果叶子没有所需的空间，请分割节点并将中间节点复制到下一个索引节点。
步骤3：如果索引节点没有所需的空间，请分割该节点并将中间元素复制到下一个索引页。

例子：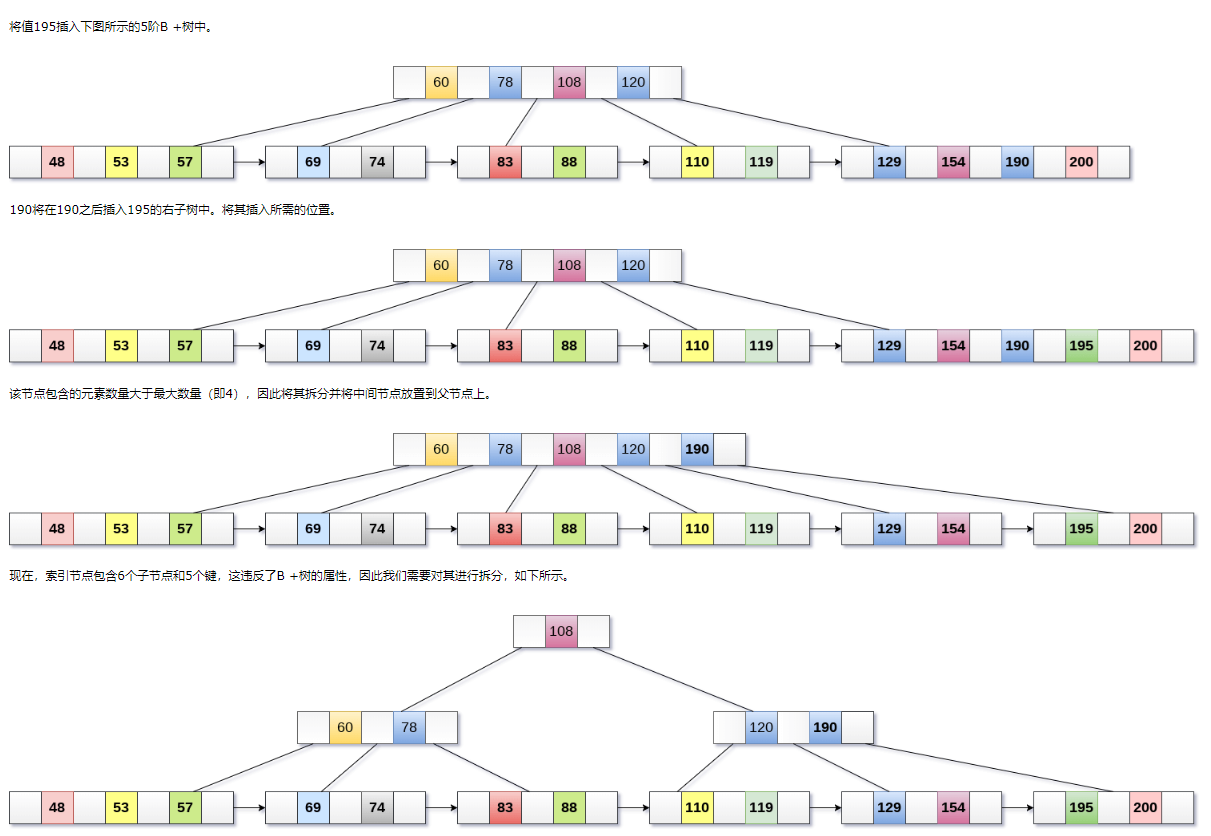
B+树插入.png

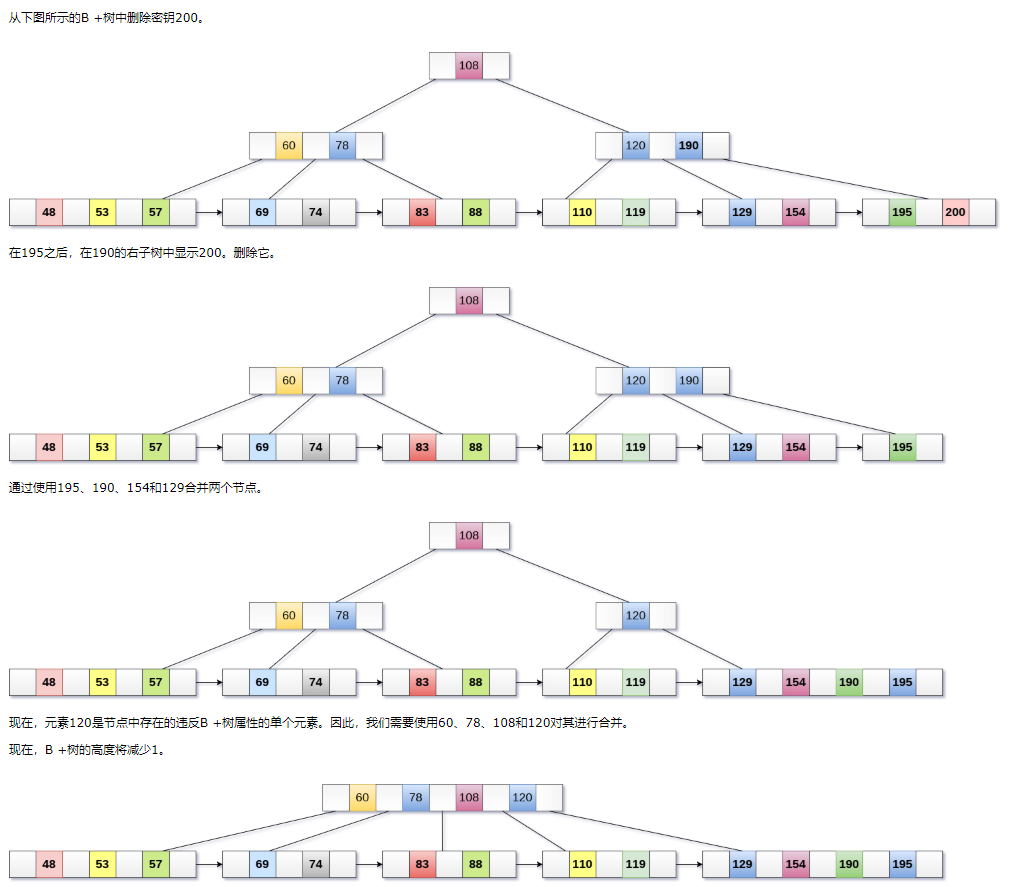
6.5、删除

步骤1：从叶子中删除密钥和数据。
步骤2：如果叶节点包含的元素少于最小数量，则向下合并节点及其同级元素，并删除它们之间的键。
步骤3：如果索引节点包含的元素数量少于最小数量，则将该节点与同级元素合并，然后向下移动它们之间的键。

例子：
B+树删除.png

tencent.jpg