堆排序
1、堆
堆是一种非线性结构,可以理解为利用完全二叉树的结构来维护的一维数组,但堆并不一定是完全二叉树。
- 每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆。
- 每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
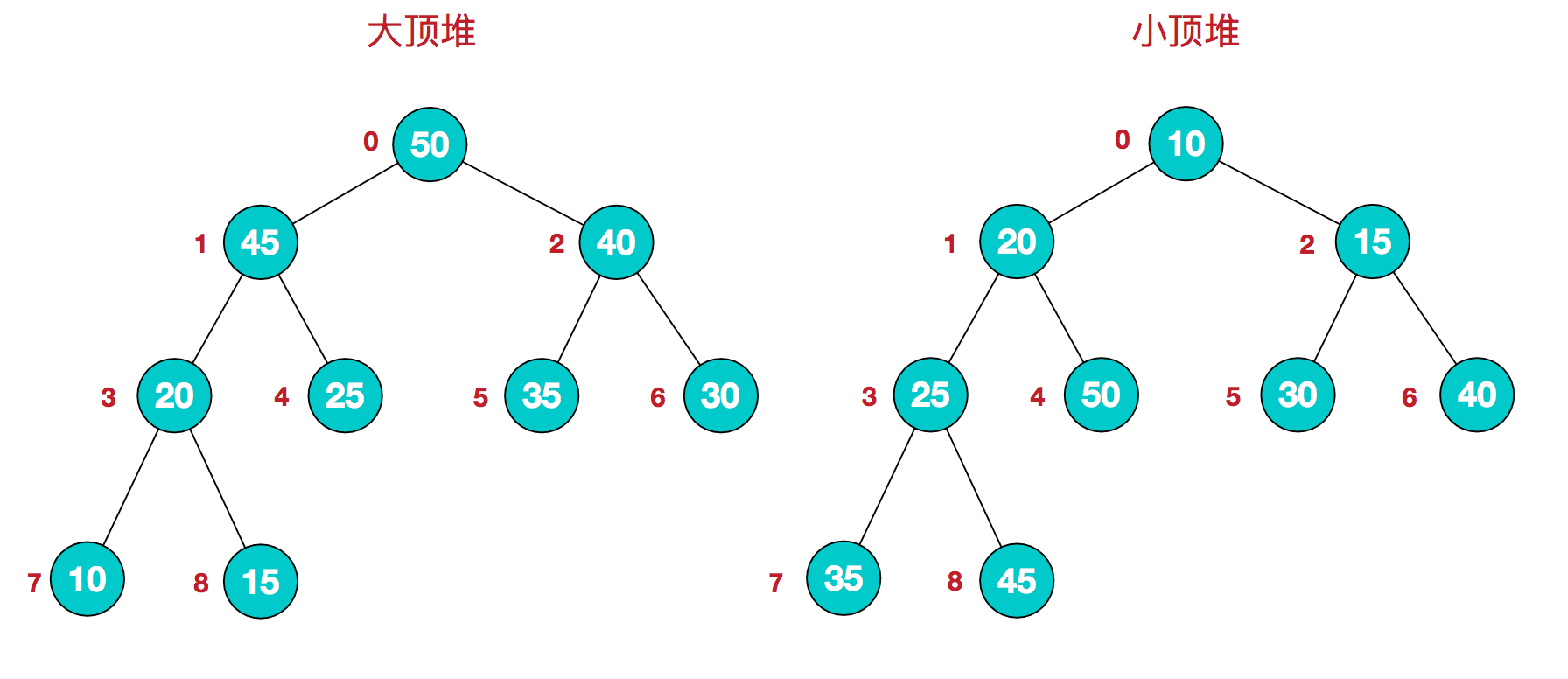
对堆中的结点按层编号,将这种逻辑结构映射到数组:

堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
2、堆排序
2.1、大顶堆排序的思想与步骤
- 将待排序的关键字序列(R1,R2,…Rn)构建大顶堆,此堆为初始的无序区.
- 将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区 (R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
- 由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆, 然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。
- 不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
2.2、动图展示

2.3、案例拆解
给定数组:[4,6,8,5,9]
2.3.1、构建初始堆
将给定无序序列构造成一个大顶堆,升序采用大顶堆,降序采用小顶堆,原因就是利用堆的性质,比如大顶堆:顶点的元素值最大,与数组末尾元素交换后,数组末尾的元素就是最大的了,再重复的调整除了末尾元素之外的其他元素成为大顶堆,再次将顶点元素与末尾元素(倒数第二的位置)交换,以此类推,这样得到的数组就是升序了。
给定无序序列如下:
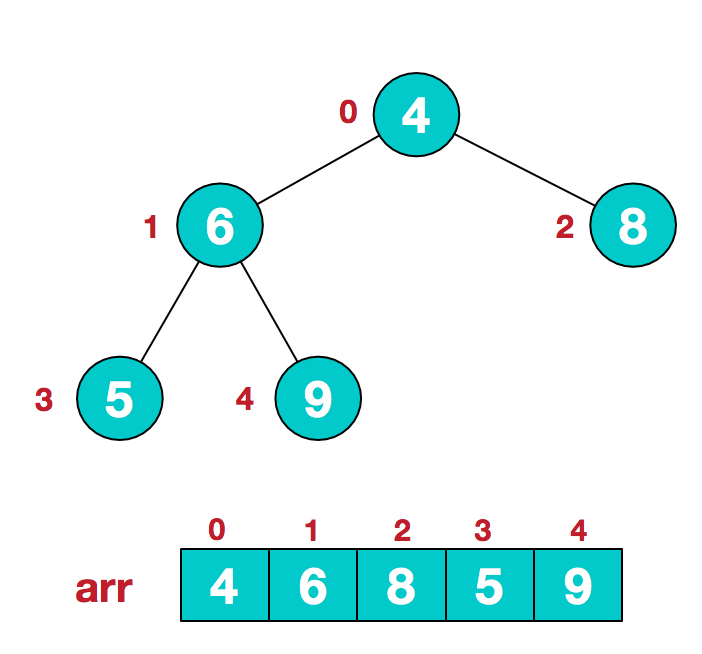
从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是值为6的结点),找到节点1的两个子节点3与4,发现最大值为右子节点4,将节点1与节点4的值交换,得到下图中的右侧结果。
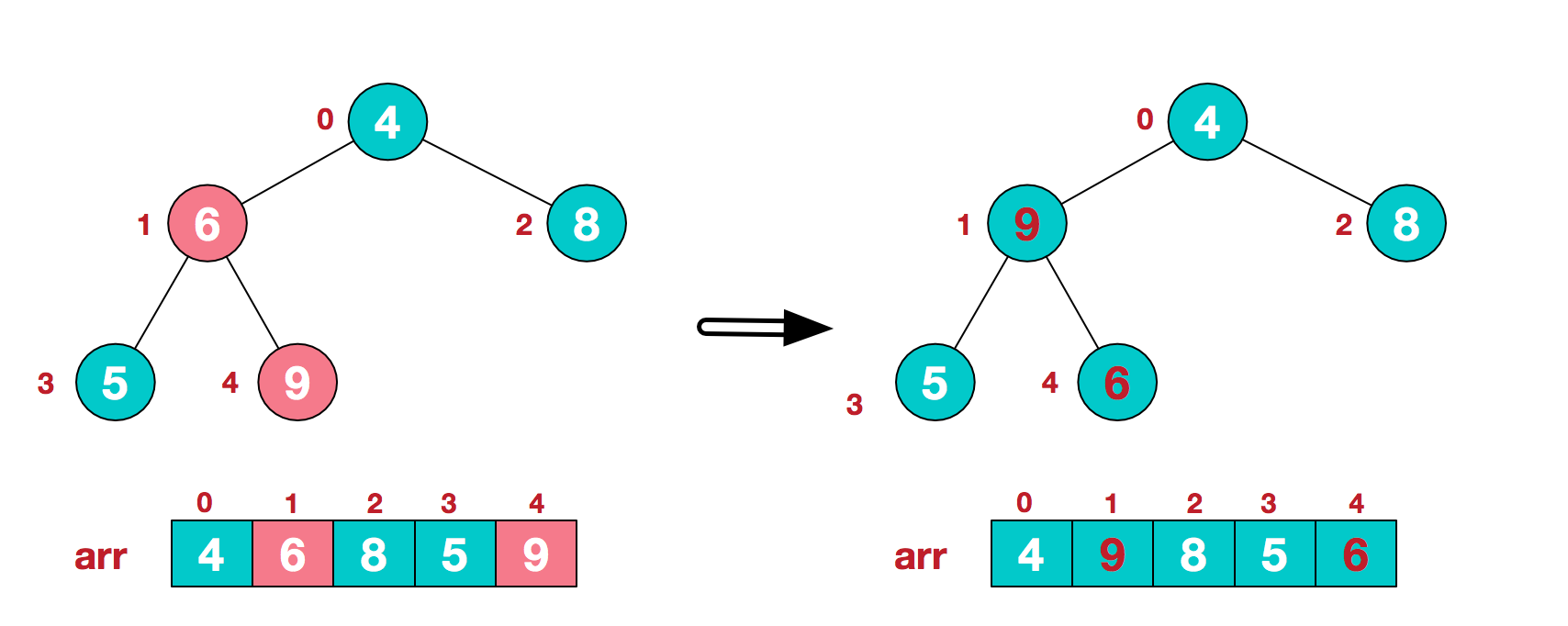
找到第二个非叶节点0(当前节点1-1=0)值为4,节点0及其左右子节点中,值最大的为0,将节点0与节点1的值4和9交换。
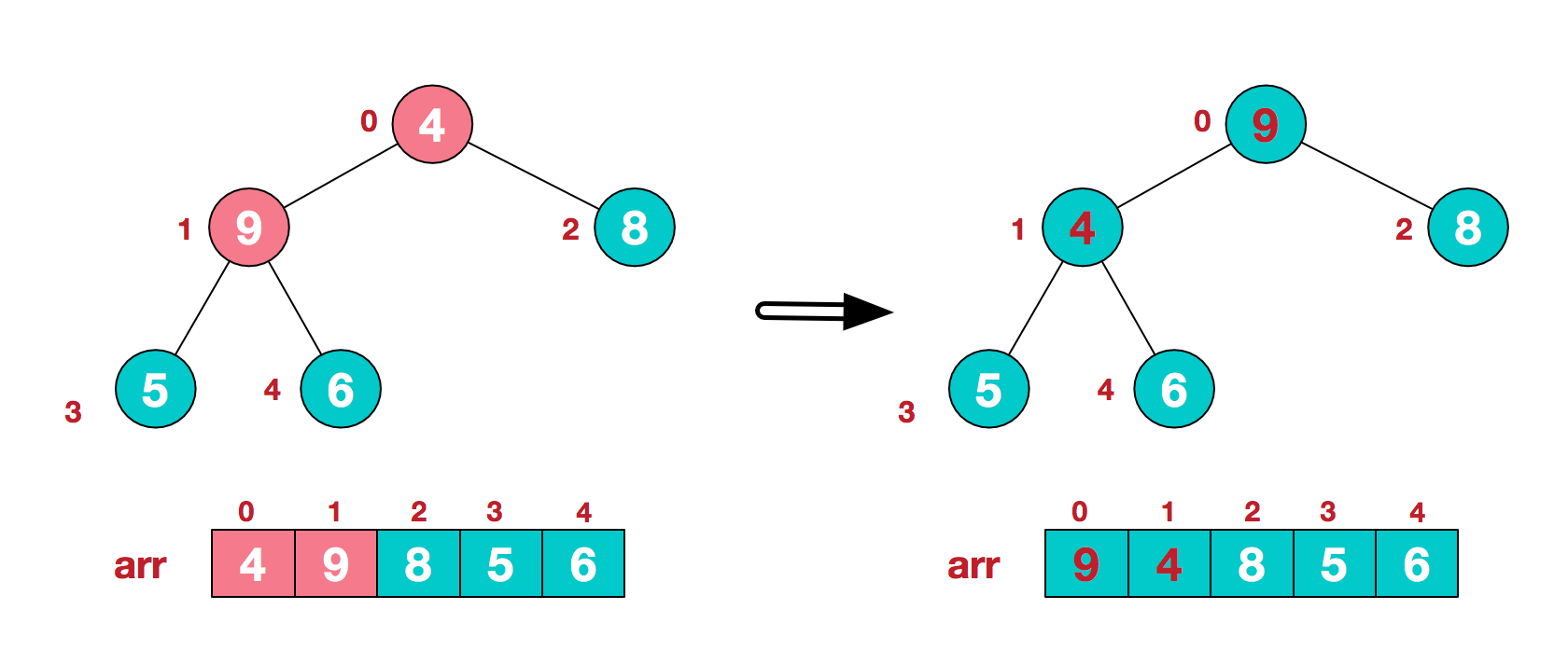
这时,交换导致了子根[4,5,6]不符合大顶堆的定义,继续调整[4,5,6],其中节点4的值6最大,交换节点1与节点4的值4和6。
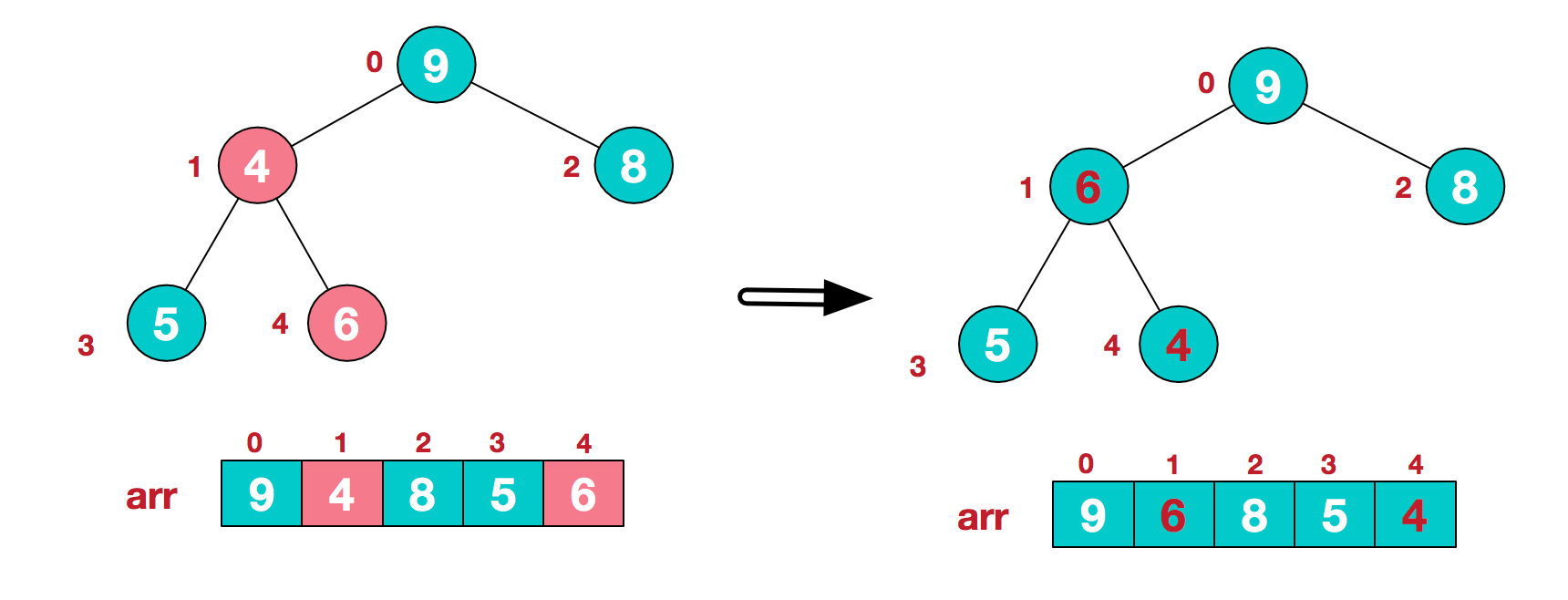
至此,我们就将一个无需序列构造成了一个大顶堆。
2.3.2、堆顶元素与末尾元素交换并重建堆
将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
将堆顶元素9和末尾元素4进行交换。
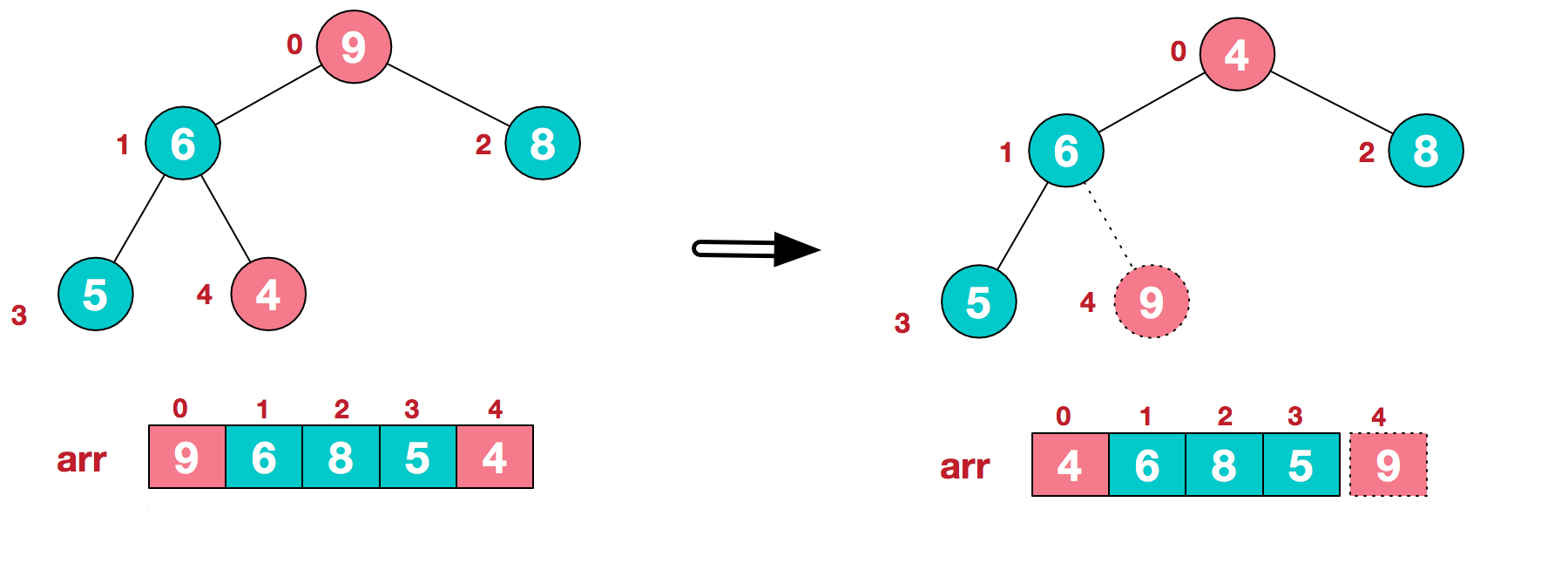
重新调整除了最后一个元素之外的其他数据,使其继续满足大顶堆的定义。找到最后一个非叶子节点( (arr.length-1)/2-1=4/2-1=1)1,其值为6,大于左子节点3的值6,无需调整,再继续找倒数第二个非叶子节点0值为4,其左右子节点中,最大值为节点2的值为8,交换节点0与2的值4和8,得到如下解结果:
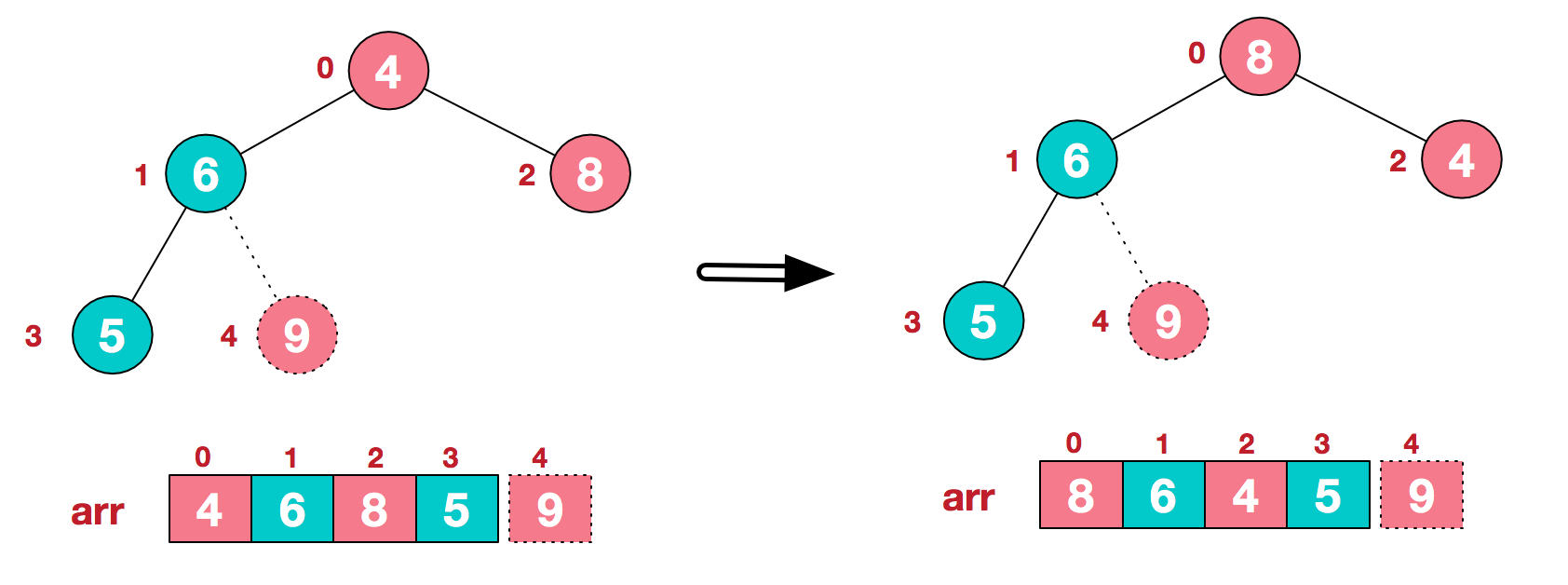
再将堆顶元素8与末尾元素5进行交换,得到第二大元素8。
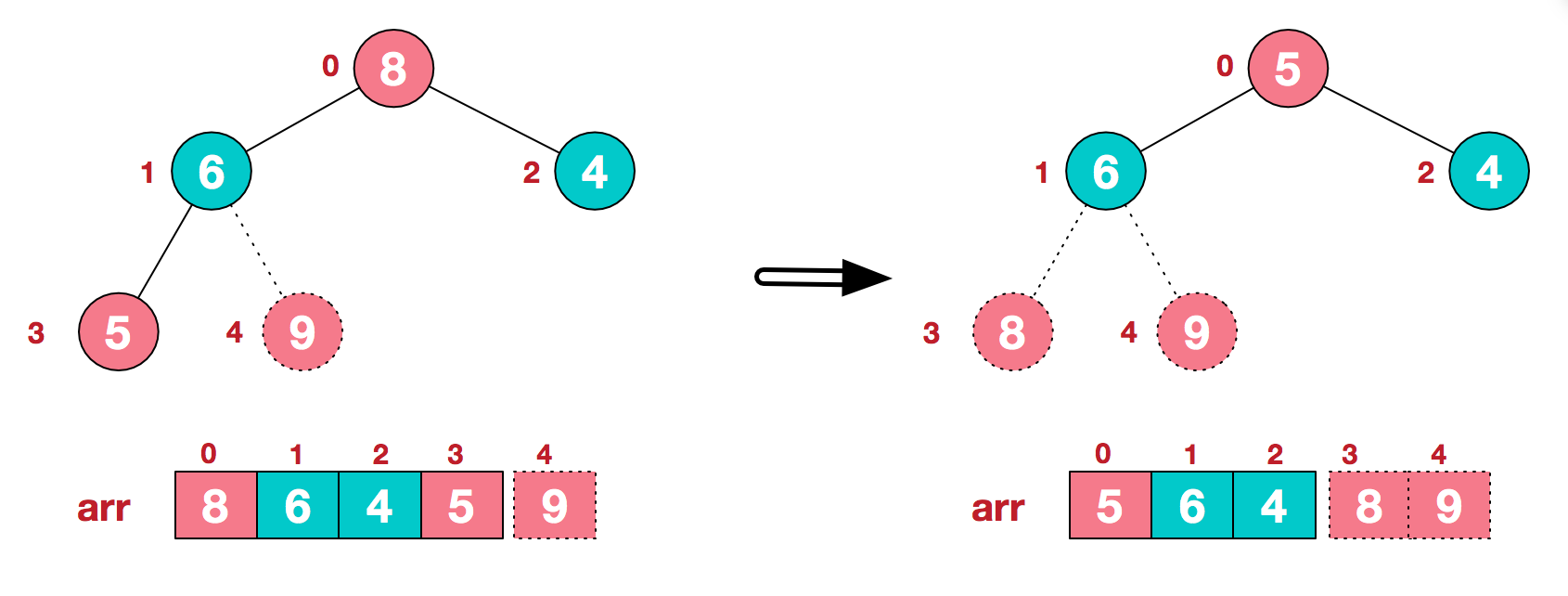
后续过程,继续进行大顶堆调整,交换,如此反复进行,最终使得整个序列有序
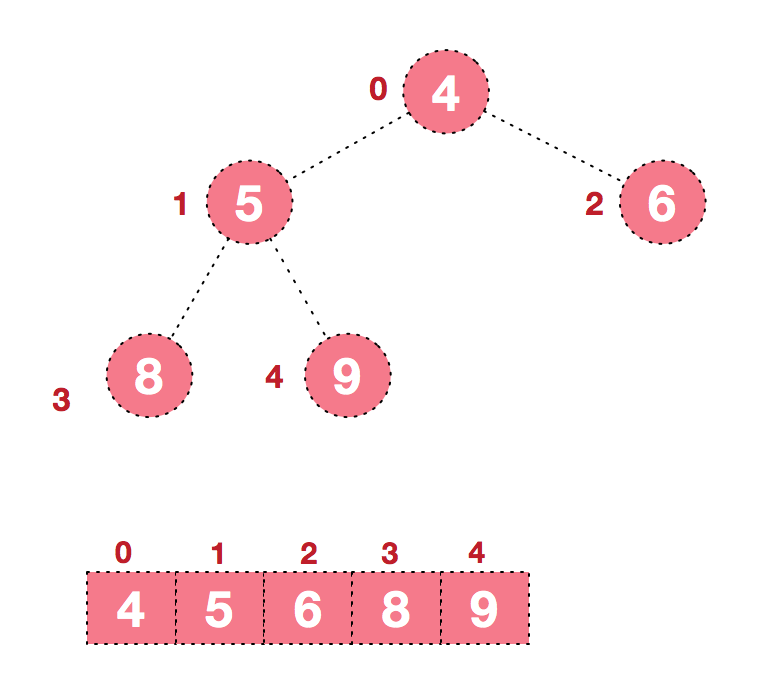
2.4、复杂度分析
2.4.1、时间复杂度
常见的时间复杂度,按数量级递增排列依次为:常数阶O(1)、对数阶O(logn)、线性阶O(n)、线性对数阶O(nlogn)、平方阶O(n^2)、立方阶O(n^3)、k次方阶O(n^k)、指数阶O(2^n)。
堆排序是一种选择排序,整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。其中构建初始堆经推导复杂度为O(n),在交换并重建堆的过程中,需交换n-1次,而重建堆的过程中,根据完全二叉树的性质,[log2(n-1),log2(n-2)…1]逐步递减,近似为nlogn。所以堆排序时间复杂度最好和最坏情况下都是O(nlogn)级。
2.4.2、空间复杂度
堆排序不要任何辅助数组,只需要一个辅助变量,所占空间是常数与n无关,所以空间复杂度为O(1)。
3、代码实现
1 | public static void main(String[] args) { |
最重要的调整大顶堆的逻辑,有两种写法:递归与循环。
1 | /** |
参考
八大排序算法——堆排序(动图演示 思路分析 实例代码java 复杂度分析)
[103 软考之堆排序](